저번 게시물에서는 디지털 회로를 설계하는 데에 있어서 가장 중요하고 기본이 되는 Pull-up & Pull-down operation에 대해서 다뤘다. 그 과정을 설명하면서 가장 기초적인 디지털 회로 중에 하나인 Inverter를 예시로 들었는데, 이번 게시물에서는 좀 더 복잡한(?) 회로에 대해서 다뤄보도록 하겠다.
CMOS (Complementary MOS) for Logic Gates
우리는 처음 Boolean Algebra를 하드웨어적으로 구상할 때 Logic Gate를 많이 이용했다. 예를 들어, 가장 흔한 논리곱과 논리합 같은 경우에는 AND, OR 등의 Gate를 사용하여 다이어그램으로 표현해왔다. 그런데, 그러한 논리 게이트들은 실질적으로 회로의 메커니즘을 한눈에 알아보기 쉽게 하기 위해 사용된 것들이었고 그 게이트 자체는 본래 여러 transistor의 조합으로 이루어져 있다. 이전 게시물에서 어떤 Input (e.g., A or B)이 회로에 인가되냐에 따라 Output이 달라질 수 있다는 것을 알 수 있었는데 그 개념을 바탕으로 우리는 CMOS라는 것을 자세히 알고 있어야 한다.
CMOS는 Complementary MOS의 약자인데, 여기서 Complementary는 직역하면 '상호보완적인'이라는 뜻을 갖고 있다. 어떤 것이 상호보완적인 건지 생각해보면, 사실 당연하게도 MOS의 종류는 P-channel과 N-channel 두 가지밖에 없기 때문에 PMOS와 NMOS가 서로 상보적일 것이라는 추측이 가능하다. 이 두 MOSFET은 과연 어떻게 상보적인 것일까?
Rule of Conduction Complements
이전 게시물에서 우리는 PMOS와 NMOS가 디지털 회로에서 각각 Pull-up Network와 Pull-down Network를 담당한다는 것을 다뤘다. 여기서부터 상보 작용은 시작된다. 오로지 0과 1로만 quantized 된 디지털 회로에서 허용 가능한 동작은 오로지 Pull-up 혹은 Pull-down 밖에 존재하지 않는다. 따라서, 회로 내부의 NMOS들이 꺼진 상태에서는 Floating 상태가 아닌 이상 무조건적으로 PMOS가 켜져 있는 상태가 되어야 한다. 이 사실을 바탕으로 Rule of Conduction Complements 라는 법칙을 설계에 적용할 수 있다.
- Pull-up Network와 Pull-down Network은 동시에 작동할 수 없다.
- 두 Network 모두 작동하지 않는 Floating 상태를 제외하고, 한 Network가 켜지면 다른 나머지 Network는 꺼지는 '상보적인' 작동이 절대적으로 지켜진다.
- 회로에서 한 Network가 Parallel connection으로 이뤄져 있다면, 나머지 다른 Network는 Series connection으로 이뤄져 있어야 한다. 반대의 경우도 마찬가지이다.
위의 세 가지 규칙에 따라서 디지털 회로는 설계된다. 사실 규칙을 어떤 계획 아래 지키려고 한다기보다, 디지털 회로 특성상 설계를 하다 보면 자연스럽게 지켜질 수밖에 없는 부분이 더 크다.
그럼 지금부터 Inverter보다 다소 복잡한 논리를 나타내는 회로 가운데 가장 흔히 보이는 것들에 대해서 자세히 알아보도록 하겠다.
NAND Gate
가장 처음으로 알아볼 논리 소자는 NAND이다. 보통 AND, OR 등을 가장 흔한 것으로 떠올릴 텐데 왜 NAND부터 소개하는지 의문이 생길 수 있다. 이는 아래의 트랜지스터 레벨의 회로도를 보면 이해를 하기 쉽다.
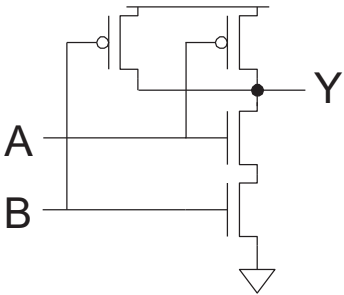
회로도를 보면 저번 게시물에 다뤘던 Inverter와 무언가 굉장히 흡사하다는 것을 알 수 있다. 자세히 들여다보면 PMOS 2개와 NMOS 2개로 이루어진 회로에 지나지 않지만, 좀 멀리서 바라보았을 때 각 Input ${A, B}$를 입력으로 갖는 2개의 Inverter 회로가 보일 것이다. 2개의 Inverter 회로이지만 특이한 점은 Output $Y$ 를 공유한다는 것이다.
이 점을 유의하며 회로의 전체적인 동작을 생각해보면, Input $A$ 와 $B$ 모두가 HIGH (간편하게 '1')가 아니라면 Output $Y$에 1이 출력될 수 있다는 것을 알 수 있다. 세부적인 예로 Input $A=0$, $B=0$ 인 상황을 들어보자면, $A, B$가 입력되는 Inverter들 모두 NMOS가 켜지지 않는 관계로 Pull-down Network가 OFF된다. 두 입력 모두 0인 경우가 아니고 한 입력만 0이 되어도, NMOS가 직렬로 연결되어있기 때문에 $Y$를 $GND$로 연결시켜줄 Pull-down Network Path가 생성될 수가 없게 된다.

위에서 Pull-down / Pull-up Network가 CMOS 회로의 전부라고 생각하면 되는데, 그중에서도 일반적인 CMOS Logic gate들의 구조는 왼쪽과 같아서 Output이 Input과 다른 상태인 경우가 대부분이다. 고로 기본적인 AND 혹은 OR 게이트와 같은 것들은 NAND, NOR에 Inverter를 하나 더 연결한 구조로 이루어지기 때문에 CMOS 회로에서는 NAND와 NOR 등이 가장 기초로 다뤄지게 되는 것이다.
이제 NAND의 Truth Table을 보게 되면, 다음과 같음을 이해할 수 있다.
| $A$ | $B$ | Pull-Down Network | Pull-Up Network | $Y$ |
| 0 | 0 | OFF | ON | 1 |
| 0 | 1 | OFF | ON | 1 |
| 1 | 0 | OFF | ON | 1 |
| 1 | 1 | ON | OFF | 0 |
NOR Gate
다음으로 알아볼 소자는 바로 NOR이다. 앞서 NAND에 대해서 설명하면서 기본적으로 다뤄야할 내용들은 모두 다뤘으므로, 여기서는 NOR의 트랜지스터 레벨 회로와 그 동작 정도를 간단하게 살펴보겠다.

왼쪽이 바로 NOR의 회로인데, 보면 위에서 다뤘던 NAND의 회로와 굉장히 흡사한 것을 알 수 있다. 다만 차이가 있다면, NOR에서는 PMOS로 이루어진 Pull-up Network가 직렬 연결이고, NMOS로 이루어진 Pull-down Network가 병렬 연결이라는 것. 이 역시 NAND가 각 네트워크가 Serial Path인지 Parallel Path인지에 따라서 결과가 달라지는 원리와 동일한 원리를 갖고 있다.
그 원리를 토대로, NOR의 Truth Table을 생각해보자.
| $A$ | $B$ | Pull-Down Network | Pull-Up Network | $Y$ |
| 0 | 0 | OFF | ON | 1 |
| 0 | 1 | ON | OFF | 0 |
| 1 | 0 | ON | OFF | 0 |
| 1 | 1 | ON | OFF | 0 |
Compound Gate
지금부터는 실질적으로 어떤 Boolean Expression을 보고 그 논리대로 회로를 생각할 수 있는 방법에 대해서 다뤄보겠다. 참고로, 어떤 조합 논리식을 보고 트랜지스터 회로를 떠올리는 데에는 어떤 정석적인 방법이라기보다 자신만의 (개인적으로 쉬운) 방법들이 있을 것이므로 내가 소개하는 방식이 정석이라고 여기지는 않길 바람.
먼저 임의의 논리식을 예로 들어보겠다.
$Y=\overline{(A+B+C) \cdot D}$ 라는 식이 있다고 가정해보자. 여기서 Input은 $A, B, C, D$ 이렇게 4가지가 있는 것을 알 수 있고, Output $Y$는 $(A+B+C)$와 $D$의 곱의 Bar여야 한다는 사실을 가장 기본적으로 알 수 있다. 여기서 어떻게 Transistor에 대한 생각을 꺼낼 수 있을까?
(1) 주어진 (혹은 필요한) Boolean Expression에서 식 전체에 해당하는 Bar가 있다면, Pull-down Network를 구현하
기 위해 전체 식에 대해 Uninverted Expression을 생각한다.
: $Y=\overline{(A+B+C) \cdot D}$ 라는 기존의 식에서 uninverted expression을 생각하면,
$\overline{Y}={(A+B+C) \cdot D}$ 가 된다.
(2) Uninverted Expression은 곧 'Pull-down Network가 Output을 $GND$로 끌어내리는' Path를 의미한다.
Pull-down Path에서, '+' (ORing)는 "Parallel" 연결을 의미하고, '$\cdot$' (ANDinig)는 "Series" 연결을 의미한다.
:

논리식에서 $(A+B+C)$ 였으므로 $A, B, C$를 Input으로 갖는 NMOS들은 서로 병렬로 연결되어 있고, $(A+B+C)$와 ANDing ($\cdot$)된 $D$를 Input으로 갖는 NMOS는 아래 부분과 직렬로 연결됨을 알 수 있다.
왼쪽과 같은 회로가 바로 이 논리식의 Pull-down Network이다.
(3) Rule of Conduction Complements 에 따라, Pull-up Network는 Pull-down Network가 이루어진 모든 구조적
인 특성과 상보적인 구조로 구현한다.
:

Pull-down Network에서 병렬로 연결된 Input들은 직렬로, 직렬로 연결된 Input으로 바꿔준 회로가 바로 Pull-up Network이 된다.
Pull-up Network까지 구현했다면, 두 Network의 Output이 서로 공유되게 연결하면 전체적인 논리식을 회로적으로 구현한 Transistor-Level Circuit이 완성된다.
앞서 "참고로"라는 말을 시작으로 언급도 했지만, 어떤 논리식을 보고 Transistor Level의 회로를 만든다는 것은 사람마다 굉장히 다를 수 있다. 누군가는 카르노 맵으로 식 자체를 최소화한 후에 구현했을 수도 있고, 누군가는 논리식 자체에 초점을 두고 회로를 구현했을 수도 있기 때문인데, 실질적으로 집적회로를 만들 때라면 면적에 대한 Cost를 낮추기 위해 최소화된 회로가 우선시되기는 한다. 하지만 그럼에도 불구하고, 이런 식으로 논리식 자체를 보고 회로 동작이 가능하게끔이라도 회로를 구현할 수 있다면 도움이 많이 될 것이라고 생각한다.
'Studies > Circuit Design' 카테고리의 다른 글
| High-Bandwidth Memory (HBM3) Specifications Study (1) (1) | 2023.07.26 |
|---|---|
| Conventional SAR ADC Design (Top-Plate Sampling) (0) | 2022.02.22 |
| Voltage Averaging with Parallel Switched Capacitors (0) | 2021.01.14 |
| Pseudo-differential Sense Amplifier (0) | 2020.09.01 |
| Transistor Level의 회로 설계 : (1) Floating, Pull-up & Pull-down (0) | 2020.07.12 |




댓글